Speed-To-Fly is one of the most important pieces of data that competition and cross-country glider pilots require to be successful. Best Glide and Minimum Sink speeds are determined by weight, wind, and air mass conditions. I have two goals in this tutorial. The first is to show you how to use the plane settings in Condor Soaring Simulator. The second, and more important, is to show you how various conditions affect speed-to-fly in real life. For most of us, we are more concerned about getting maximum distance while flying cross-country. Condor’s Polar utility offers a fantastic visual aid to assist the real world pilot in understanding Glider Polars, and use them to properly interpret speed-to-fly. This document uses the Condor Plane Settings function to illustrate how the various factors affect the glider’s Polar curve.
Helmut Reichman in his excellent book “Cross-Country Soaring” states that: “If you never land out you are being too conservative and if you are landing out most of the time you are not conservative enough”.
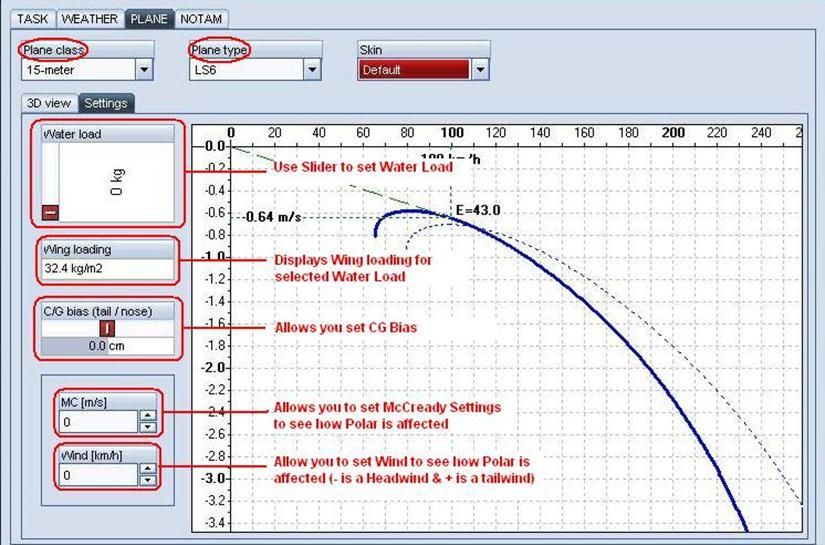
So let us look at the Plane settings screen in Condor:
Plane Class: This allows you to select the Class of Glider you will use for the task. In this case I have chosen to use the 15 meter Class. If you are setting up a multiplayer task then all players are forced to use the same class as you have chosen.
Plane Type: This allows you to choose a particular model within the Class. In this case I have chosen LS-6.
Water Load: You can move the slider to adjust your water load. For good conditions and fast speeds use more water. For poor conditions and thermalling use little or no water. Note that you can dump water in flight while in the simulator therefore it is a good idea to start out with water.C/G Bias: This allows you to choose to make minor adjustments to the C/G. Range is -10cm (Tail Bias) to +10cm (Nose Bias). Use Tail bias if you intend to do a lot of thermalling, and use Nose bias if you are going to be speeding along in wave or ridge lift. This adjustment will not affect the glider performance (Polar).
MC (m/s): This allows you to choose adjust McCready settings. This is useful to determine polar speed-to-fly in various air mass conditions. 1 m/s is ~ 2 knots (1.94) or 200 ft/min (196.9)
Wind (km/h): This allows you to set a headwind (-) or tailwind(+) component to see how it affects the speed-to-fly.
The graphical area of the Plane Settings screen is where we get the information that we require:
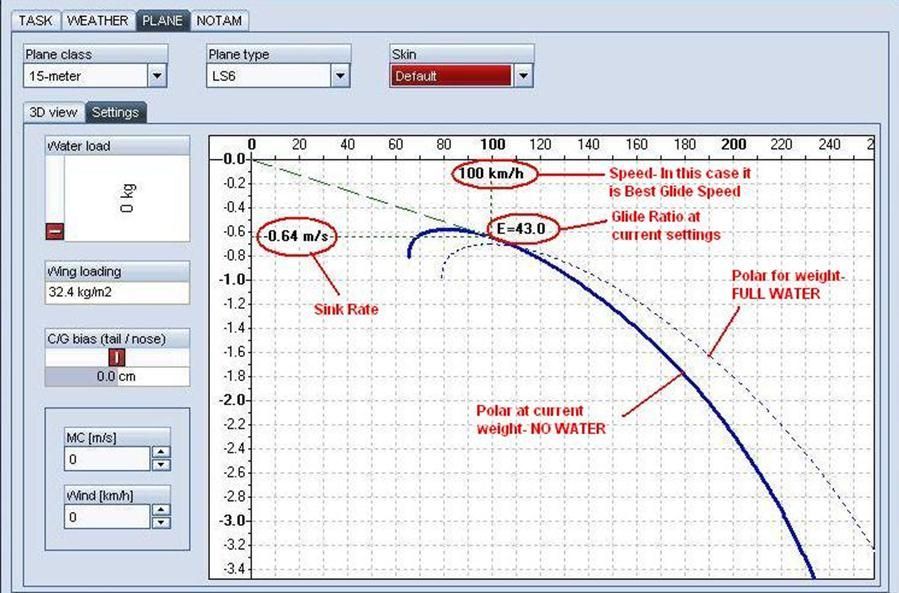
As you can see we are able to determine Sink Rate, Speed-to-Fly, and Glide Ratio based on the settings we have entered. In this case the LS6 with no water has a ratio of 43:1, and will give us 0.64 m/s (1.2 knots) of sink when flown at the Best glide speed of 100 kph (54 knots).
These first two illustrations are essential to setting up your virtual glider for a Condor task. We can use this screen to show how the Polars in Condor are affected. Real life Polars are affected in the exact same manner. The rest of this document illustrates speed-to-fly as determined by the Polar curves and the various factors affecting performance.
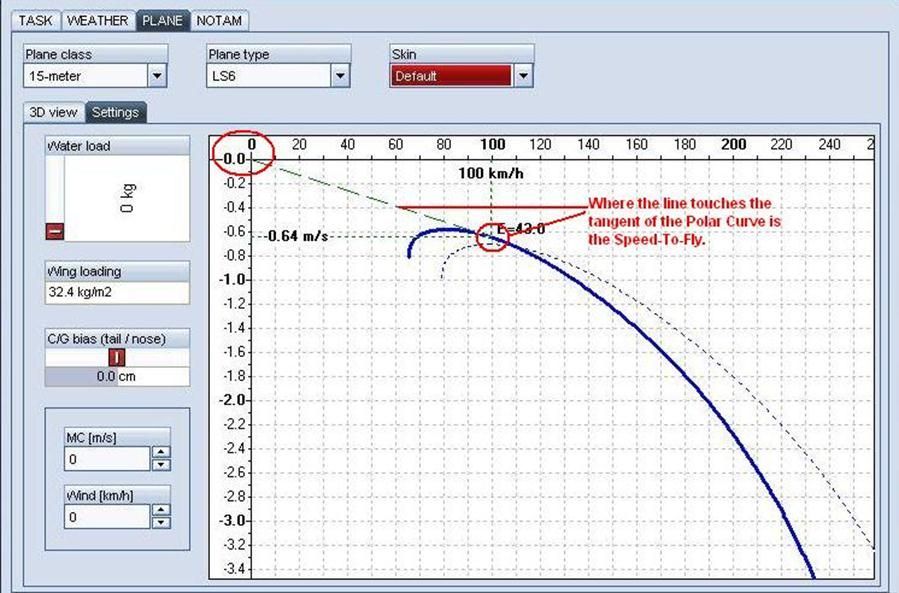
It is important you know how to read the Polar to determine speed-to-fly. The dashed line that runs from the sink and speed coordinates, tangent to the curve, is what determines our speed-to-fly.
In this particular case we are provided a very important piece of data. If a line is drawn from the 0/0 coordinates to a tangent on the Polar, where it touches is the Best Glide speed. In this case in the LS6 with no water, stable air mass (no lift or sink), and no wind, our Best Glide is 100 kph (54 KTAS). This will result in a Glide Ratio of 43:1 if we maintain that true airspeed.
Best Glide speed is the speed-to-fly to cover the maximum amount of distance.
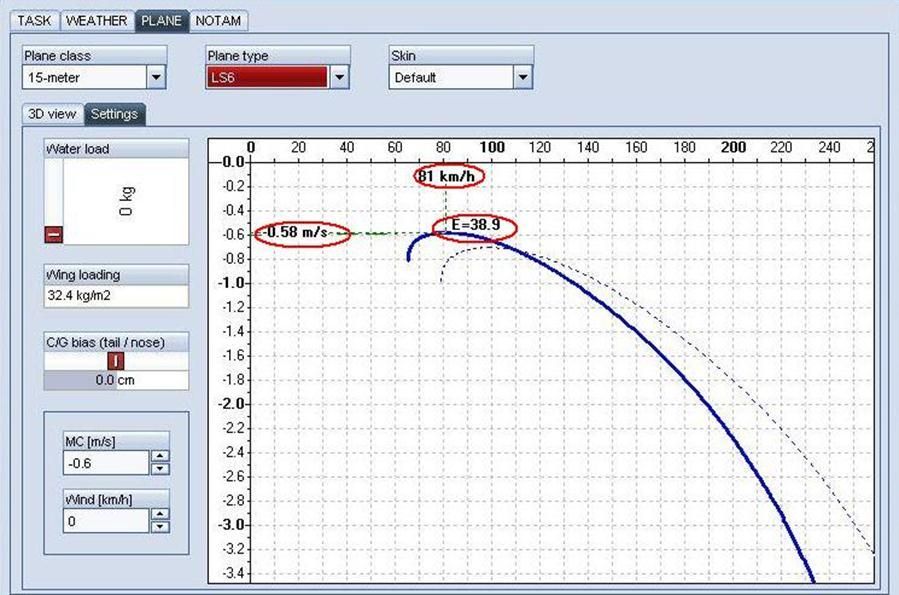
Now we want to determine our Minimum Sink Speed. To do this we adjust the MC setting so that it matches our sink rate:
In this case we attempt to match the MC setting as closely as possible to the sink rate. In real life you would draw a flat horizontal line from the tangent of the Polar to the sink index. Here we have a MC setting of -0.6 and a sink rate of -0.58. Close enough for our purposes. The Speed-To-Fly given is our Minimum Sink speed of 81 kph or 44 KTAS. Flying this speed will result in a Glide Ratio of 38.9:1
Minimum Sink speed is the speed-to-fly for maximum endurance and/or climb in lift. It should be flown when thermalling or trying to gain the most altitude in lift. It is also the speed-to-fly for minimum altitude loss.
This is a very valuable visual of how Glider Polars work in real life. The difference in real life is that you have to use the gross weight of the glider and adjust the Polar accordingly. In Condor the gross weight without water is pre-determined and the only way you can change weight is to add water.
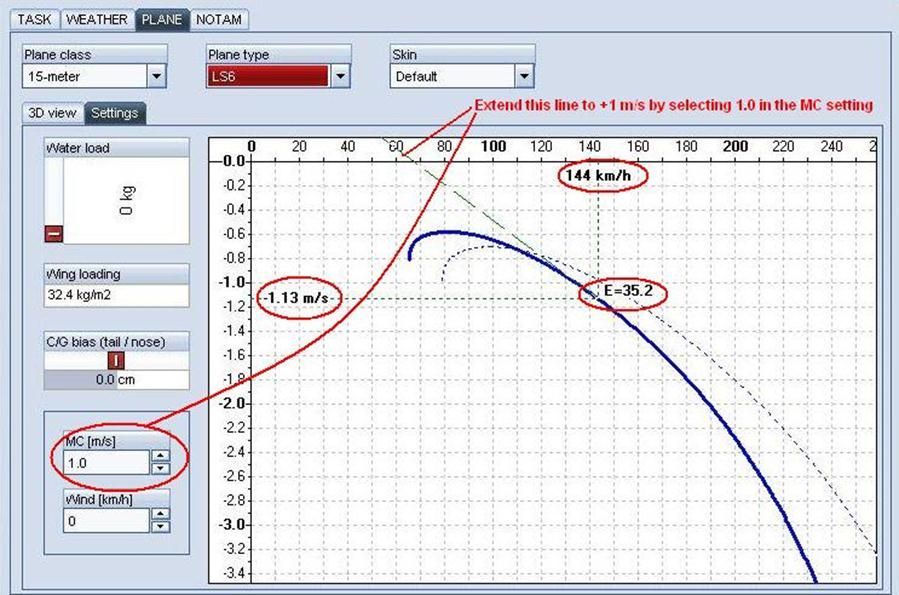
As a general rule of thumb we want to fly slower in lift and faster in sink. This is for obvious reasons as you want to get out of sink as quickly as possible, and stay in lift as long as possible. We can use our Polar to determine the best speed-to-fly for just about any given situation. For example, let us say that we have 2 knots of sink (1 m/s):
In real life you would extend the graph upward to 1.0 and draw your tangent line. In Condor simply selecting +1.0 in the MC will perform the same action. In this case you can see that the best glide speed-to-fly is 144 kph or 78 KTAS. This will result is a sink rate of 1.13 m/s (2.2 knots) and a glide ratio of 35.2 though still air. You must also factor in the sink rate which is 1 m/s. Thus your true sink rate is 2.13 m/s (4.4 knots) and so your real Glide Ratio in this case is 18.8!
If you fly slower than this you are going to stay in the sink for a longer period of time, losing both distance and altitude. If you fly faster, you are going to lose excessive altitude. The idea is to cover as much distance as possible, in the shortest time period, with minimum altitude loss.
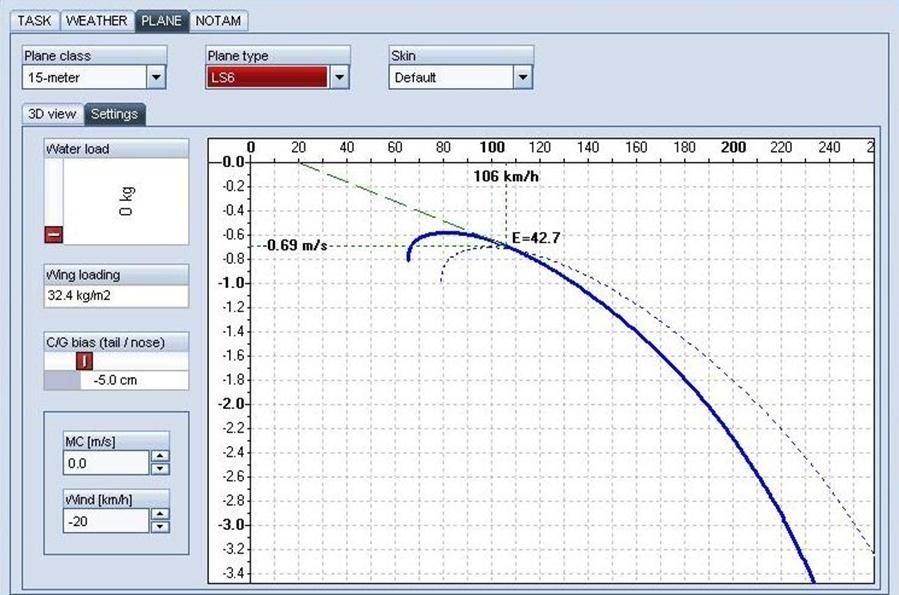
Wind will also greatly affect the speed-to-fly. As a general rule of thumb you fly slower with a tailwind and faster with a headwind. As a rule of thumb you should not fly slower than minimum sink in a tailwind. The stronger the headwind the faster you should fly. The rule of thumb is to increase your airspeed by 50% of the wind i.e. if you have a 20 knot headwind increase your speed by 10 knots. In the case where we are flying in no sink at best glide and had a headwind of 10 knots we would want to fly at 59 KTAS (54 + 5). We can see a good visual of this by looking at the Polar:
Here you can see that a headwind component of 20 kph (10.8 knots) has shifted our tangent line. According to the Polar, our Best Glide speed-to-fly is 106 kph or 57.2 KTAS which is very close to our rule of thumb speed of 59 KTAS.
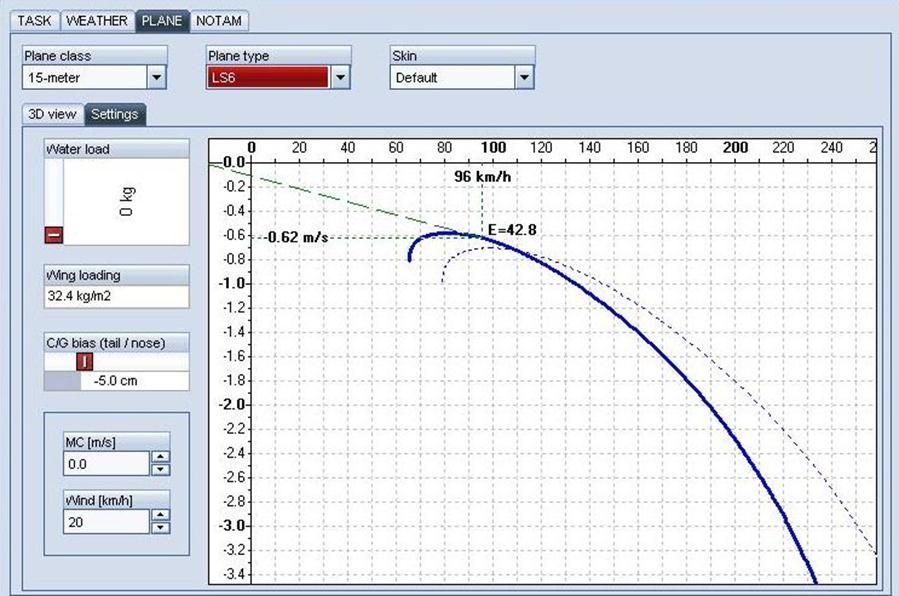
Now let us look at a 20 kph (10.8 knot) tailwind:
As you can see from our Polar the Best Glide Speed to fly is now 96 kph or 52 knots.
Again as previously mentioned there is no reason to fly less than Minimum Sink speed even in stronger tailwinds.
Next we will take a look at how weight affects our Polar.
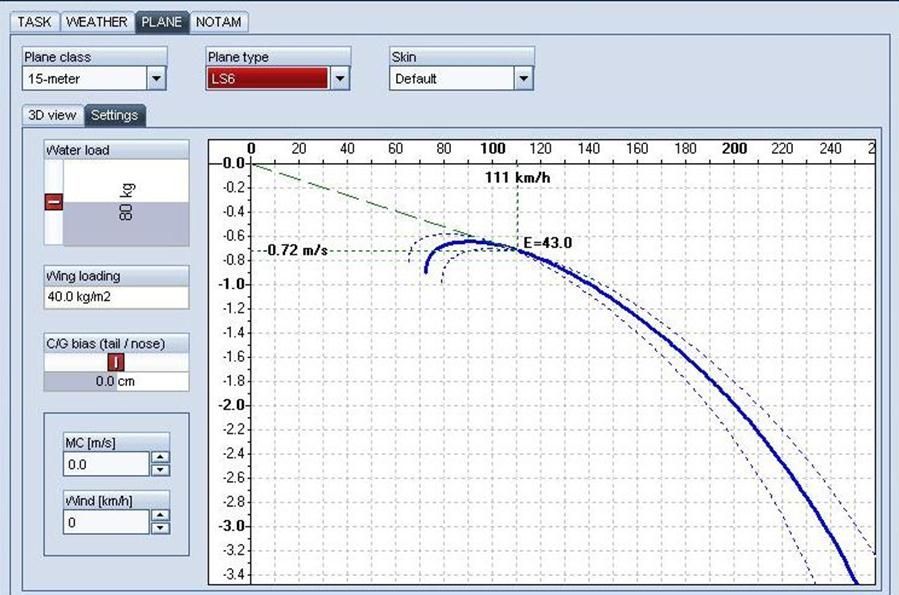
Let’s start loading up the LS6 with water. At 50% load we have increase our weight by 80 kg (176 lbs). You can see the shift in the Polar curve:
This results in a Best Glide of 111 kph (60 KTAS), glide ratio of 43:1, and a sink rate of 0.72 m/s (1.4 knots). Note that compared with the “no water weight” Polar, the speed and sink rate have both increased, however the Glide Ratio is still that same.
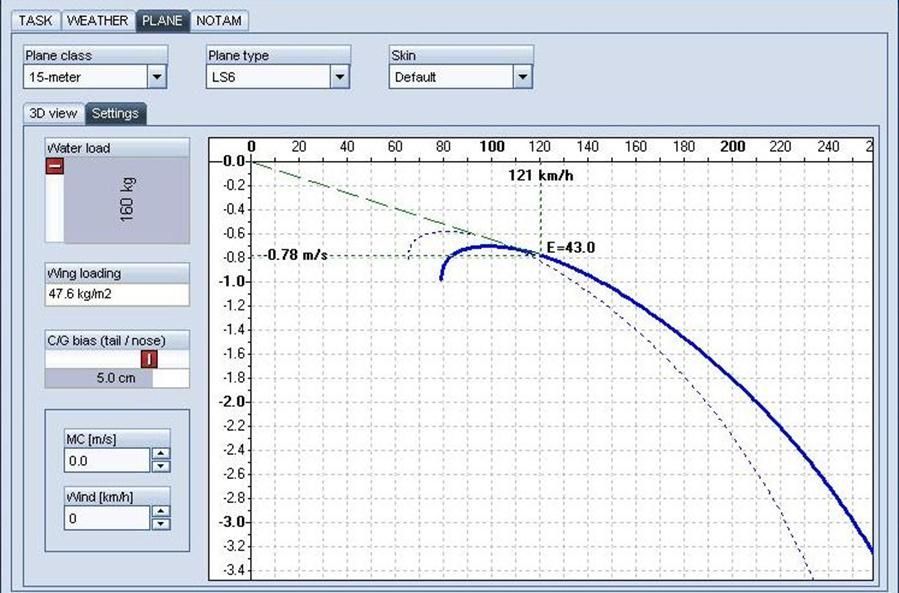
Now let us look at a full water load. Our weight has increased by 160 kg (353 lbs). We are now at the maximum gross weight for the glider:
This results in a Best Glide speed of 121 kph (65 KTAS), glide ratio of 43:1, and a sink rate of 0.78 m/s (1.5 knots). Again note that the speed and sink rate have both increased, however the Glide Ratio is still that same. A glider will always have the same glide ratio regardless of weight. As you increase weight, the best glide speed and sink rates will increase, but the ratio will be the same.
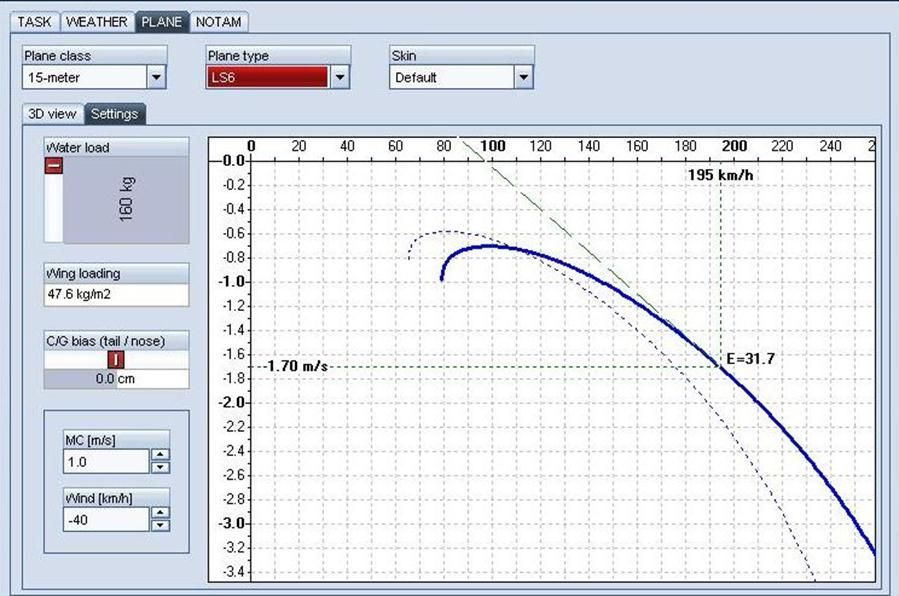
Now for an in-flight illustration. We are flying with 100% Water Load (max gross) in a sink of 1.9 knots (1 m/s), and a headwind of 21 knots (40 kph):
As you can see from the graph, both sink and the headwind result in an increase to our Best Glide speed-to-fly. In this instance Best Glide is 195 kph (105 knots), with a sink rate of 1.7 m/s (3.3 knots) and a glide ratio of on 31.7:1 for this glider in still air. Factoring in our sink rate of 1.0 (m/s) our actual sink rate is 2.7 m/s (5.2 knots) giving us a true glide ratio of just 20.1!
Now this all looks rather complicated given all the variants that can and do exist. Fortunately, both in Condor and in real life, we have computers and PDA’s that do these calculations for us in real time. I believe, however, it does help for you to understand the basic theory.
I have purposely left out discussion about McCready Theory as it requires its own in-depth study.
I hope this tutorial has aided you in better understanding Glider Polars thru the visualization that Condor offers. I found Bob Wander’s “Glider Polars & Speed To Fly” to be a good reference on this subject. Also Helmut Reichman’s excellent book “Cross Country Soaring” should be a part of any soaring pilot’s library.
In addition I would like to include a discussion about True Airspeed, Indicated Airspeed, and Flutter. Indicated Airspeed is equal to True Airspeed only at sea level with a Standard atmosphere. The ICAO (International Civil Aviation Organization) standard atmosphere at MSL (Mean Sea Level) is defined as 15° C, 1013.25 hectaPascals, and with a lapse rate of 1.98° C per 1000 ft. Translated to Imperial Units, this is 59°F, 29.92 in hg, lapse rate of 3.56°F. As a basic rule of thumb, TAS will increase by 2% per 1000 ft increase in Pressure altitude given in the formula:
TAS = IAS + (IAS)(.02) (Alt/1000).
For our purposes we will use KIAS (Knots Indicated Airspeed) and KTAS (Knots True Airspeed).
Example:
Altitude = 10,000 ft
IAS = 100 KIAS
TAS = IAS + (IAS)(.02) (Alt/1000) = 100 + (100)(.02)(10,000/1,000) = 120 KTAS
For example let’s say we have an altimeter setting of 30.52, indicated altitude of 10,000 ft is 59°F. Using our trusty E6B (or in my case Sporty’s Electronic Flight Computer) we can determine that:
Pressure Altitude = 9451 ft
Density Altitude = 11581 ft
TAS = 119.3 KTAS
Thus you can see that our 2% rule is close enough to use in general flight.
For simplification you can determine Pressure altitude by correcting the altimeter setting to the standard of 29.92 in hg. If the altimeter setting is higher, then you subtract. If it is lower, then you add.
Example:
Altimeter setting = 30.52
30.52 – 29.92 = 0.60
0.60 x 1000 = 600ft
30.52 is higher than 29.92 so we subtract the correction factor:
10,000 ft – 600 ft = 9400ft Pressure Altitude
Of course the simplest way of determining Pressure Altitude is to change your altimeter to 29.92 and the altimeter will display pressure altitude.
TAS = IAS + (IAS)(.02) (Alt/1000) = 100 + (100)(.02)(9400/1,000) = 118.8 KTAS
As you can see, the simple rule of thumb calculations that you can do mentally are close enough to use in flight.
The reason for this discussion is that at True Airspeeds above redline we can induce a phenomena known as Flutter. This causes a harmonic oscillation in the wings, control surfaces, or fuselage that will result in structural failure if not immediately brought under control. Google “sailplane flutter” and you will find some interesting and eye opening videos. This can be simulated in Condor. Start at an altitude of 10,000 ft and start a dive steep enough to reach redline. You will hear a distinct noise, and if you keep it up, the glider will break apart and you will see a message stating that “(Your Name) has tested flutter”. Our ASW-19b experienced flutter in real life and an AD was issued as a result. This incident happened before we owned it. As a result our Glider is specifically exempted by serial number from the AD.
Thing to remember:
- For maximum distance fly at the Best Glide speed as determined by the conditions.
- For maximum endurance fly at Minimum Sink airspeed.
- For maximum altitude gain in lift fly at Minimum Sink airspeed
- In a headwind increase your airspeed by 50% of the headwind component.
NOTE: Basic McCready Theory does not take wind into account. - An increase in the weight of the Glider results in an increase in the Best Glide and Minimum Sink airspeeds
- A decrease in the weight of the Glider results in a decrease in the Best Glide and Minimum Sink airspeeds
- A glider will always have the same glide ratio regardless of weight.
- Pressure Altitude is Indicated Altitude corrected for non-standard pressure.
- Density Altitude is Pressure Altitude corrected for non-standard temperature.
- To determine Pressure Altitude adjust your indicated altitude by 1000 ft for every 1.00in hg.
- As a rule of thumb TAS (True Airspeed) increases by 2% for every 1000 feet of pressure altitude.
- For lift and sink 1 m/s = 2 knots = 200 fpm (not exact but close enough)







2 comments for “Polars and Speed-to-Fly Using the Condor Simulator”