I’ve been torn in my efforts to fly faster lately. For a few years, I’ve been working hard to better follow “energy lines.” I’ve been trying to emulate my buddy Herb Kilian at the Chicago Glider Club, who is regularly wipes us all off the scoresheet by floating along in lift while I bore a hole in the sky. But then came Ephrata, and a long set of conversations with Bill Elliott. He’s been trying to go as straight as possible to minimize course deviations, and obviously that’s working great for him. Maybe I’m wandering too far around the sky? Who is right? Now that flying season has been replaced by goof-off-at-the-office season, it’s time to think it through. Here are some principles I’ve come up with.
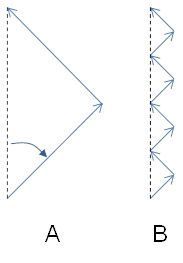
Degrees matter, not miles. Many pilots measure their deviations by how many miles they have gone off course. This is a mistake. The only thing that matters is how many degrees you go off course. Figure 1 illustrates. Pilot A and B each travel the same amount of extra distance. But pilot A goes many more miles off course than pilot B.
Small deviations are cheap. The cosines of small angles are very large. In Figure 1, the length of the dashed courseline is not much much less than the glider’s path for quite large course deviation angles. The table below gives some numbers: A 10 degree deviation costs almost nothing. Even a 30 degree deviation is only a 13% loss in efficiency. Once past 45 degrees though, the costs start to spiral up dramatically. Going more than 45 degrees off course is really costly.
| Deviation: | 0 | 10 | 20 | 30 | 45 | 60 | 90 |
| Efficiency: | 100% | 98.5% | 94.0% | 86.6% | 70.7% | 50% | 0% |
Table 1. Loss of efficiency for flying off course. The efficiency numbers are 100×cos(θ).
To get further, we have to measure the benefits against these costs. As usual everything in racing comes down to MacCready theory. (See Upwind and downwind and Just a little Faster Please at http://faculty.chicagobooth.edu/john.cochrane/soaring/.)
Let’s start with the question, “How far should I go off course if I can cruise through lift that way?” You may want to follow a cloud, a street, a lift line, or a ridge at an angle to the courseline, and so on.
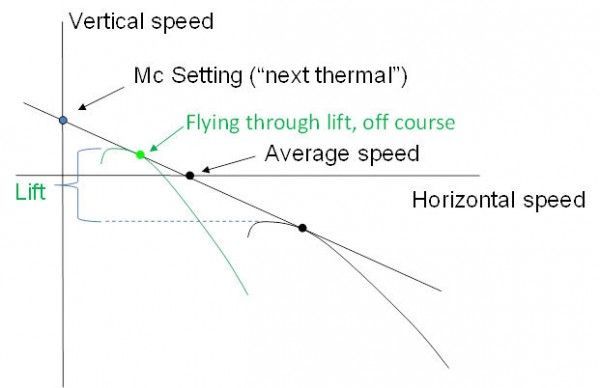
Figure 2 gives the answer. Start with the classic MacCready theory. The curved black line is the glider polar, showing its sink as a function of airspeed. The straight line starts at the MacCready setting — the “next thermal” in books, but really the “weakest thermal you’d stop for right now.” The tangent to the polar gives the speed to fly. The point marked “average speed” is just that. If, as in this case, your thermal lift is the same as your sink in cruise, then average speed is half the cruising speed.
Now, flying off course is the same as accepting a slower glider, shown in the green polar. It moves the polar to the left. (V′=Vcos(θ).) Flying through lift moves the polar up, reducing the sink rate. The pictures shows a case in which the green polar moves up and to the left just enough that the average speed point doesn’t move. In this case, you’re just indifferent to plowing ahead on course, versus flying off course in a “slow” glider, but through lift. If you can find lift better than this, go off course. If the lift is worse than this, then plow on ahead.
Figure 1 gives a sense that course deviations to follow lines of lift will pay off for modern gliders. Our polars are really flat. If you’re cruising at 40:1, 80 knots, sinking 2 knots and Mc 2 in still air (typical), the MacCready line has a slope of 20:1. Thus, you’d go off course for a deviation that gives on knot more vertical speed even if it cuts the horizontal speed down by 20 knots. Now, 20/80 = 25%, so that’s about 40 degrees off course in table 1! In an older glider, the MacCready line is steeper, so course deviations will not pay off so well — you need more lift in order to trade a KA6 in for something even slower.
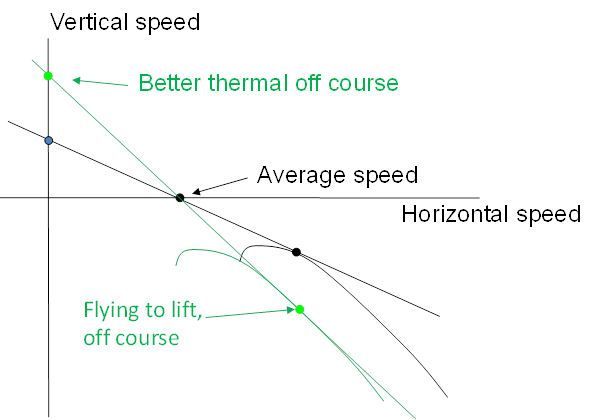
The other question we might ask is, “suppose I can fly through the same (still) air off course to a better thermal. Is it worth it?” Figure 3answers that question.
A better thermal is represented by raising the intercept of the MacCready line. Now, we only shift the polar to the left, as you’re flying a “slower glider” but not flying through any better air to get to the thermal. Again, it’s just worth it if the average speed is the same.
We need numbers. Here are the formulas (algebra on my website) for these two questions. I assume the pilot flies a steady speed rather than MacCready speeds when chasing the “better thermal.” Most of us fly a constant speed, and it simplifies the formulas a lot. Then, a pilot is just indifferent between flying straight ahead to a knot thermal, versus flying off course by θ degrees to a stronger knot thermal, when is given by 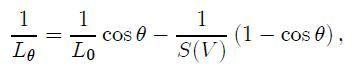 where S(V) denotes the sink rate at cruising speed V.
where S(V) denotes the sink rate at cruising speed V.
Our pilot is also just indifferent to flying straight ahead through lift or sink versus flying off course θ degrees through steady lift or sink , if ia given by
![]() where is the MacCready setting, or next thermal for both course options.
where is the MacCready setting, or next thermal for both course options.
Anyone awake? Let’s look at some plots. Figure 4 answers the question, is it worth going off course to find a better thermal? Here’s how to read it. Suppose you are gliding straight through still air, and you think the next thermal ahead will be 2 knots (2 knot MacCready setting.) How far off course should you go if you think there is a 3 knot thermal over there? Follow the green line, which starts at 2 knots on the vertical axis. Keep going until the green line rises to 3 knots, and look down to find the answer, which is about 35 degrees. So, it’s worth going up to 35 degrees off course to climb at 3 knots rather than fly straight ahead to climb at 2.
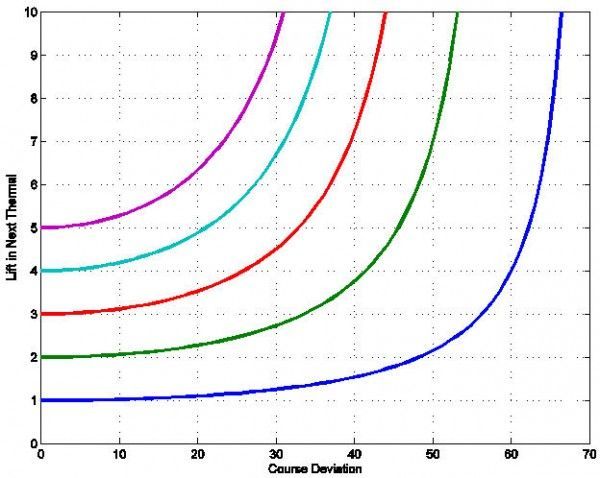
Caption: Figure 4. is it worth going off course to find a better thermal? For each MacCready value, the line indicates how much better thermal off course makes a course deviation worthwhile.
The plot carries a number of lessons:
Small deviations are nearly costless. The lines each start on the left at the thermal the pilot will find straight ahead, but they start moving horizontally to the right. It’s worth making small — 10-20 degree course deviations for even very slightly better thermals.
Make smaller deviations in stronger weather. If you can find a 5 knot thermal straight ahead, you need to know there is a 10 knot thermal to make a 30 degree course correction worthwhile! Bill is right at Ephrata, where thermals were strong but isolated.
Make big course deviations in weaker weather. Herb is right in Chicago. Here it is typical to find two knots straight ahead, but 3-4 knots if you go chasing clouds. That means up to 30-40 degree course deviations are ok.
Make really big course deviations in very weak weaker. If you’re going to end up climbing at 1 knot, it’s worth really going anywhere to avoid that fate. Even 50 degrees off course for a 2 knot thermal is justifiable.
This is part of the general point: Avoid weak lift. It’s much better to climb at 3 knots always than to have half your thermals at 1 knot, and half your thermals at 5 knots. Minutes per foot matter, not feet per minute.
Don’t go past the wall. Each line explodes vertically off the chart at some point. If you fly sufficiently far off course, you go slower than flying straight and taking a 2 knot thermal, even if you can find an infinitely strong thermal off course.
Figure 5 asks the other question: Suppose you have a chance to glide through lift off course to get to the next thermal. How far off course should you go?
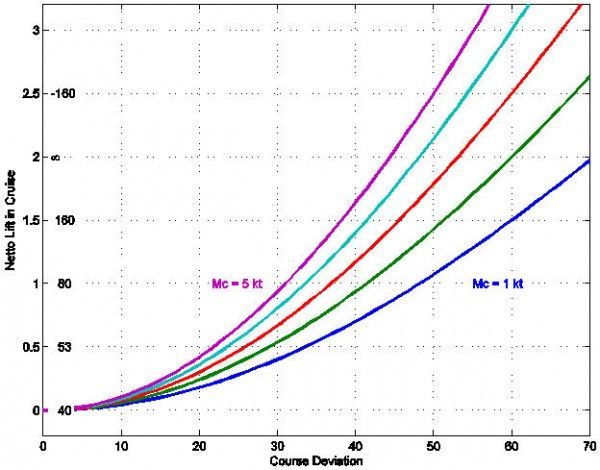
Caption: Figure 5. How far off course should you go to cruise in lift? The left vertical axis meausures netto lift experienced in the off-course glide. The right hand vertical axis measures the achieved L/D in the off-course glide.
Start again with the green line which represents a 2 knot thermal ahead. Follow it out to 40 degrees and 1 knot. That means it’s worth going up to 40 degrees off course if you can do it in 1 knots (netto) lift rather than still air. Again, stronger lift — higher McCready settings — mean smaller deviations. 1 knot lift only justifies 30 degrees for Mc 5, 40 degrees for Mc 2 and 50 degrees for Mc 1.
Assessing the vertical axis is harder here. How big is big? 1 knot of airmass (netto) lift is not a huge amount — it means your vario will say about 1 knot down rather than 2 knots down in still air. It means your speed director will say to fly about 10 knots slower, 65 knots (dry) rather than 75 knots. On the other hand, most of the time you don’t get 1 knot of smooth lift. You are more likely to fly off course to bump a cloud, or to fly along a line with both lift and sink. To use the 1 knot line you have to average 1 knot lift the whole way.
Many pilots like measure their glide abilities with achieved L/D, so I stated the vertical axis in those units as well, assuming an 80 knot cruise speed. (My baseline here is an L/D of 40 at 80 knots, with 2 knots sink.) Thus, the 1 knot average netto lift is the same thing as being able to achieve a LD of 80, and justifies the rather substantial course deviations in order to follow lines of lift. A more typical (Eastern) achieved glide of 53 still justifies 20-30 degree course deviations.
If you can follow really good lift, where you don’t lose altitude at all (infinite L/D, 2 knots netto up) then 40 degrees is permissible even at Mc 5, and dramatic deviations in the rest of the country! Here we see an invitation to stray, even in strong lift. Uvalde offers a chance to follow lift lines, and even if the thermals are quite strong, it’s worth making substantial course deviations if you can follow lift lines. Maybe Herb is more close to right at Uvalde.
These lines do not explode vertically. Yes, there is a point where a 90 degree course deviation is permissible. That point is, if you can fly straight through lift that is as strong or stronger than the next thermal. After all, when you thermal you have no forward component either.
In summary, it’s worth taking much bigger course deviations to fly through lift than to fly to lift.
Avoid sink! If boring ahead to the next thermal involves going through sink, it’s even more worth taking a deviation. Figure 6 supposes that you have to go through 1 knot sink on average to go straight to the next thermal. I chose 1 knot sink because I seem to get about 30:1 on poorly chosen glides on thermal days. Really bad sink leads to even bigger deviations.
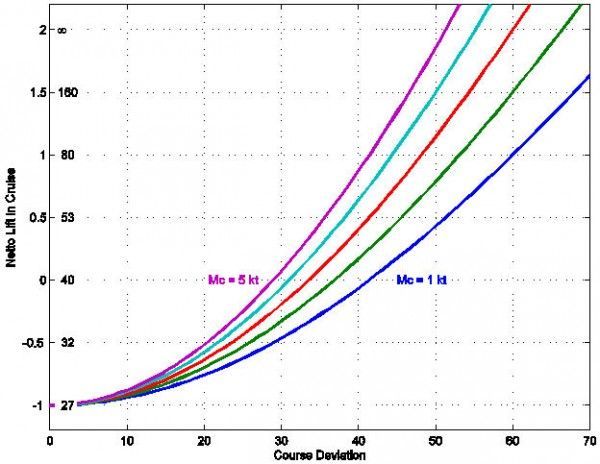
Caption: Figure 6. The value of course deviations when the pilot must fly through 1 knot netto sink ahead.
For example, follow the 0 netto lift or 40:1 glide line to the right, and you see that even with a 5 knot thermal ahead, (purple) it’s worth deviating by 30 degrees just to fly in still air. If you have a 2 knot thermal ahead, it’s worth a 40 degree deviation. It’s even worth deviating 20-30 degrees just to get reduced sink — half a knot rather than a knot, or achieve 32:1 rather than 27:1. Again, D/L, minutes per foot, are really the right units. If you can avoid sink and fly through lift instead, that justifies huge course deviations.
So, what’s the bottom line, fly like Herb or fly like Bill? For most cases, 20-30 degrees off course seems pretty sensible if you have decent indications of lift in that direction. Only go more if it really looks good and/or conditions are pretty weak. Never go more than 45 degrees off course unless you’re climbing all the way in lift as strong as you’d thermal in.
What about wind? Wind changes things a lot — going off course into the wind is a lot less costly than going off course down wind. Strong winds can justify dramatic course deviations. That’s part II!
This looks hard. Do we really need the numbers, and not just to grow birdbrains? Yes. Go see Moneyball. Gliders are all about the same, and the pilots are all excellent. The only way to win at this sport is to fly really precisely. These kinds of tradeoffs — go 20 degrees off course to one cloud or 30 to another — are all quantitative, and would take centuries of experience to figure out right.
We don’t all have to do the math though. If we can get quantitative guidelines like these (and Upwind and downwind) implemented in flight computers and distilled for practical guidance, we can fly just that little bit faster and more consistently that it takes to win contests.
[Editor’s note: If you are interested in seeing all the math, it can be found at the end of the article, Deviations Part I , on John’s website.]
Let the SoaringCafe.com community know what you think about deviating to maximize cruise by providing comments below. Perhaps a dialog on the subject can help others understand this better. — the Editors







2 comments for “Deviations, Part I”